[자료구조] 네이버 부스트코스 '자바로 구현하고 배우는 자료구조' 공부 필기 (1)
자료구조를 본격적으로 공부하기 위해 아무 강의나.. 무료로 있는 강의를 들어보기로 했다.
출처 강의 : '자바로 구현하고 배우는 자료구조', Rob Edwards, https://www.boostcourse.org/cs204/joinLectures/145114
자바로 구현하고 배우는 자료구조
부스트코스 무료 강의
www.boostcourse.org
약간 앞부분만 먼저 들어봤는데 좀 초보가 듣기에는 어렵게 설명을 하시는 것 같다.
하지만 어차피 뭐든 물어볼 수 있는 구글이 있으니까 일단 계속 들어보기로 했다.
※ 강의를 들으며 개인적으로 필요한/기억해둘 내용 + 더 잘이해하기 위해 찾아본 내용만 필기했음
자료구조 학습 목표 : 자료를 효율적으로 처리하고 구조화하는 능력 향상
(목표를 봐도 알겠지만, '자료구조'는 '알고리즘'과 비슷하지만 다른 과목이다)
여담으로, Rob Edwards 선생님.. 개인 유튜브 채널도 있으시단다.
https://www.youtube.com/watch?v=zgCnMvvw6Oo&list=PLpPXw4zFa0uKKhaSz87IowJnOTzh9tiBk
- 본 강의에서는 연결 리스트, 스택/큐, 체인 해시, 트리, 여러 정렬 방식에 대해서 학습할 예정이라고 함
1. 복잡성 소개
[개요]
- 많은 양의 데이터를 "잘" 관리하고, "효율적으로" 처리하기 위해 자료구조와 알고리즘이 개발되어 왔음
- 여기에서 "효율적"이라는 단어의 의미는?
- "효율적이다"를 판단할 수 있는 기준은?
- 우리는 "시간 복잡도"를 통해 알고리즘의 효율성을 비교할 수 있음
[내용]
- 여러 알고리즘을 비교 해봐야하는 순간이 있음
(e.g. 이 상황에서는 어떤 알고리즘이 더 좋을까 고민할 때 등등)
- 이때 우리는 '서로 다른 알고리즘의 효율성을 비교'하기 위해서 "시간 복잡도"를 사용함
- 그리고, 이 '시간 복잡도'에는 몇가지 규칙이 있음
- 첫번째. 입력값은 항상 0보다 크거나 같다
→ 음의 입력값은 가질 수 없음 (시간 복잡도를 고려할 때 말이 되지 않음)
- 두번째. 함수는 입력값이 많을 수록 더 많은 작업을 한다
→ 당연하게도 많은 요소가 입력되면 함수는 더 많은 작업을 해야함(여기에서 "작업"의 의미는 나중에 공부함)
- 세번째. 시간복잡도에서 "상수"는 고려하지 않는다
→ 가령, 시간 복잡도가 3n인 알고리즘이 있다고 하면, 이 알고리즘은 시간 복잡도가 n인 알고리즘과 같다는 의미
→ 즉, 시간 복잡도가 n인 알고리즘이 시간 복잡도가 3n인 알고리즘보다 더 오래걸리는 알고리즘이 아니라는 이야기임
- 네번째. 낮은 차수 항은 무시한다
→ 여기 x축은 n, y축은 시간인 그래프가 있음
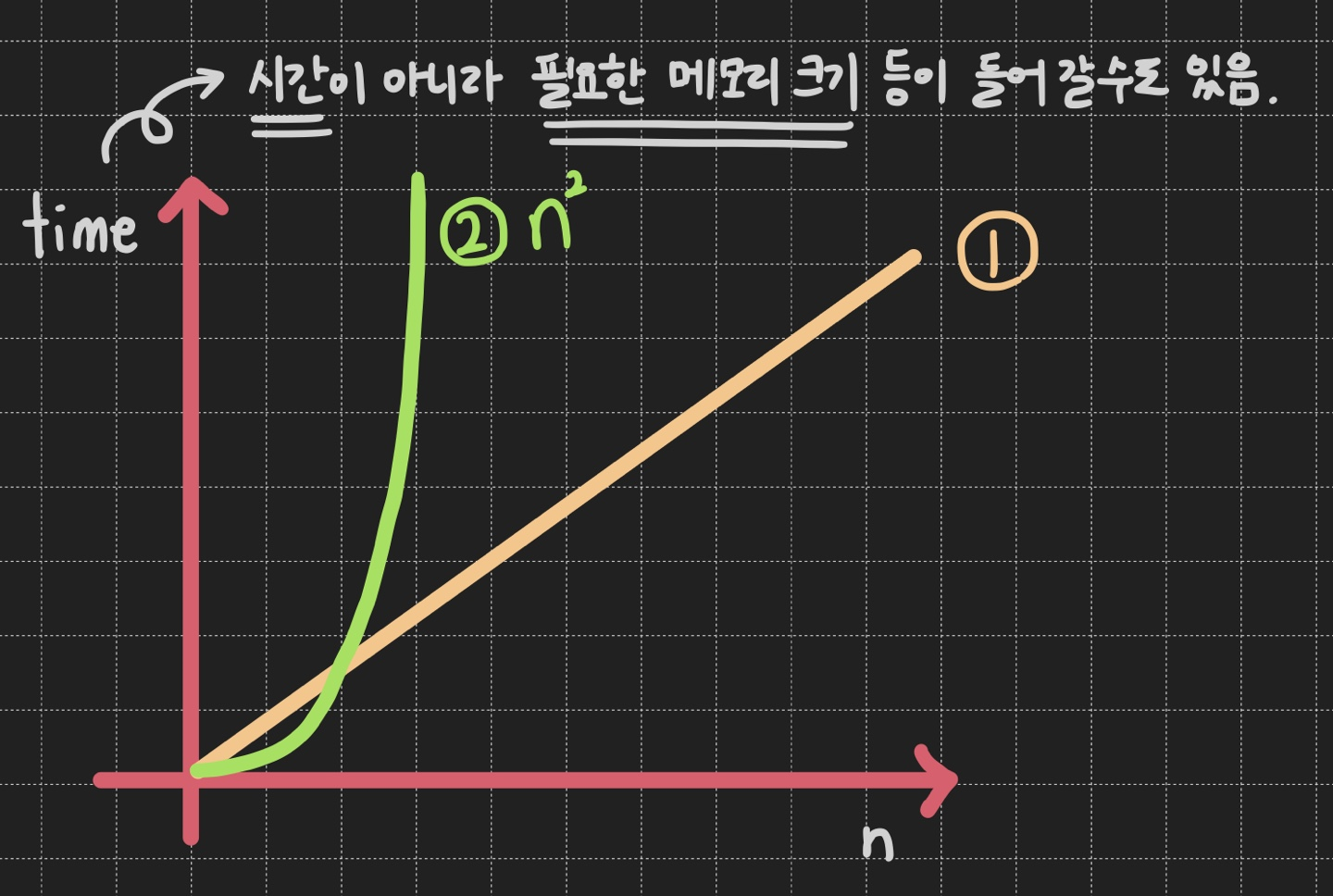
→ 그리고, n이 증가함에 따라 시간도 선형적으로 증가하는 알고리즘이 있다고 가정 (그래프 ①)
→ 또 다른 알고리즘은 n^2라고 가정 (그래프 ②)
→ 즉, n과 n^2 알고리즘이 있는 상태이고, 두 그래프가 만나는 지점은 n=1일 때일 것임
→ 하나의 작업을 처리하는건 어렵지 않기 때문에 1보다 작은 상황에 대해서는 알고리즘을 생각하지 않음
우리는 n이 무한대로 커진다는 경우를 가정하고 알고리즘을 비교해야함
→ 그래서 시간복잡도에서 낮은 차수의 항은 무시하기로 함 (즉, n^3 + n^2 + 5 라는 항이 있을 때 n^3만 고려함)

- 다섯번째. 시간 복잡도가 로그일 때, 로그의 밑은 무시한다
→ 모든 로그는 서로 배수 관계임
→ 따라서 시간 복잡도가 로그인 알고리즘을 비교할 땐 로그의 밑을 무시해도 됨
→ 참고로 복잡도가 log인 알고리즘은 자료를 반으로 나누거나, 2를 곱하는 경우라고 함
→ 예시. 이진탐색
(알고리즘의 시간 복잡도를 비교할 때는 로그의 밑인 "2"를 무시함)
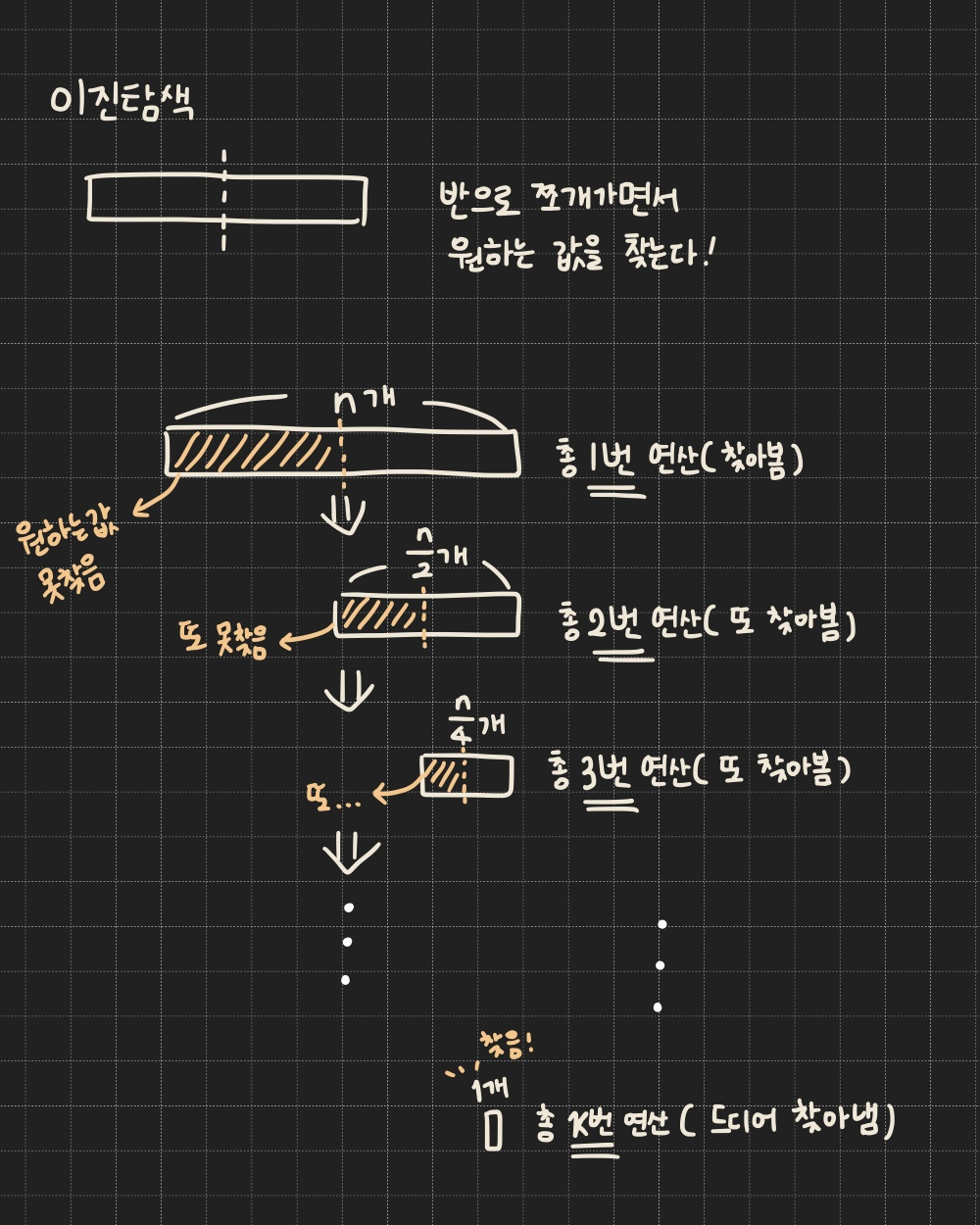

→ 즉, 위의 이진탐색의 시간복잡도는 logN이 됨 (로그의 밑 무시)
→ 중요한 점은 "시간 복잡도에 대해서 이야기할 때 로그의 밑을 무시"한다고 말하는 것임
당연히 수학에서는 절대 무시하면 안됨..
→ 그리고 팁으로.. (아마 쓸모 없을 것 같지만) 로그의 밑이 다른 값을 비교해야한다면 로그의 성질을 이용하면 됨

- 여섯번째. 등호를 사용한다
→ 다음 시간에 배우겠지만 2n = O(n) 임
→ 이 식의 뜻은 2n이 어떤 함수의 집합에 속한다는 뜻임
→ 여기에서 등호는 "속한다"는 의미가 됨