회고록 블로그
[자료구조] 네이버 부스트코스 '자바로 구현하고 배우는 자료구조' 공부 필기 (2) 본문
자료구조에 대해서 공부하고 있다.
출처 강의 : '자바로 구현하고 배우는 자료구조', Rob Edwards, https://www.boostcourse.org/cs204/joinLectures/145114
자바로 구현하고 배우는 자료구조
부스트코스 무료 강의
www.boostcourse.org
이전 필기 내용 :
2021.11.05 - [2. 개발 공부/CS 공부] - [자료구조] 네이버 부스트코스 '자바로 구현하고 배우는 자료구조' 공부 필기 (1)
[자료구조] 네이버 부스트코스 '자바로 구현하고 배우는 자료구조' 공부 필기 (1)
자료구조를 본격적으로 공부하기 위해 아무 강의나.. 무료로 있는 강의를 들어보기로 했다. 출처 강의 : '자바로 구현하고 배우는 자료구조', Rob Edwards, https://www.boostcourse.org/cs204/joinLectures/14511..
cinnamonc.tistory.com
1. 빅 오 표기법
[개요]
- 알고리즘의 효율성을 "수학적으로" 표시하는 빅 오 표기법
[내용]
- 빅 오 표기법(Big Oh Notation)?
→ 두 알고리즘을 비교하고 싶거나 어떤 알고리즘이 얼마나 효율적인 알고리즘인지 표현하고 싶을 때 빅오 표기법을 사용함
- 빅 오(Big Oh)는 컴퓨터 과학에서 가장 많이 사용되는 용어 중 하나이기도 함
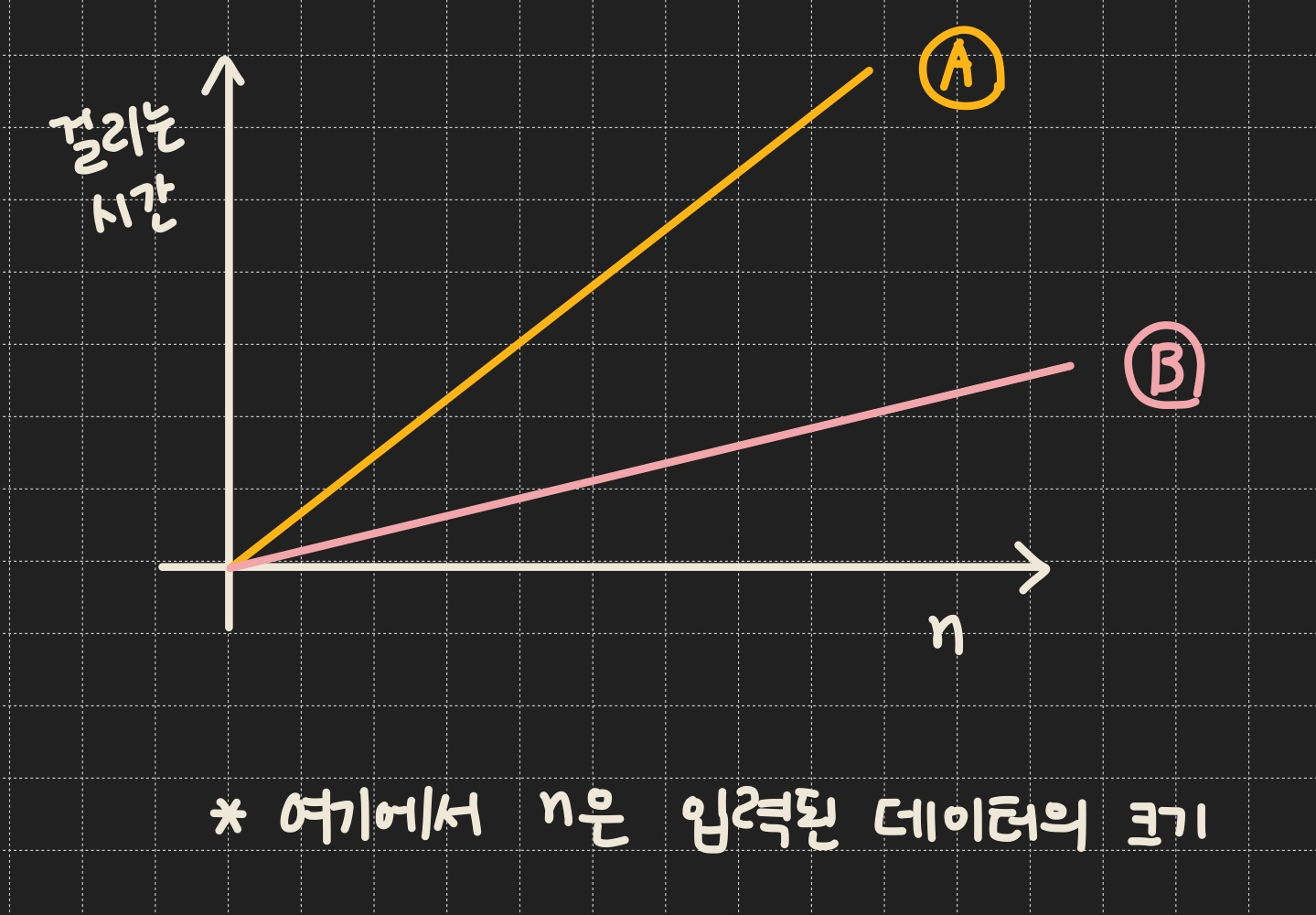
- 아래와 같은 그래프가 있다고 가정하자 (그림1 참고)
→ 그래프 A를 기준으로 해서 그래프들을 비교하고 싶음 (여기에서 그래프 A의 함수는 n임)
→ 같은 크기의 데이터(n)를 처리하는데 그래프 B가 그래프 A보다 더 적은 시간이 걸림 (= 그래프B가 더 빠른 알고리즘)
→ 여기에서 그래프 A보다 같거나 더 빠른 알고리즘(= 그래프 B)을 빅 오로 나타낼 수 있음
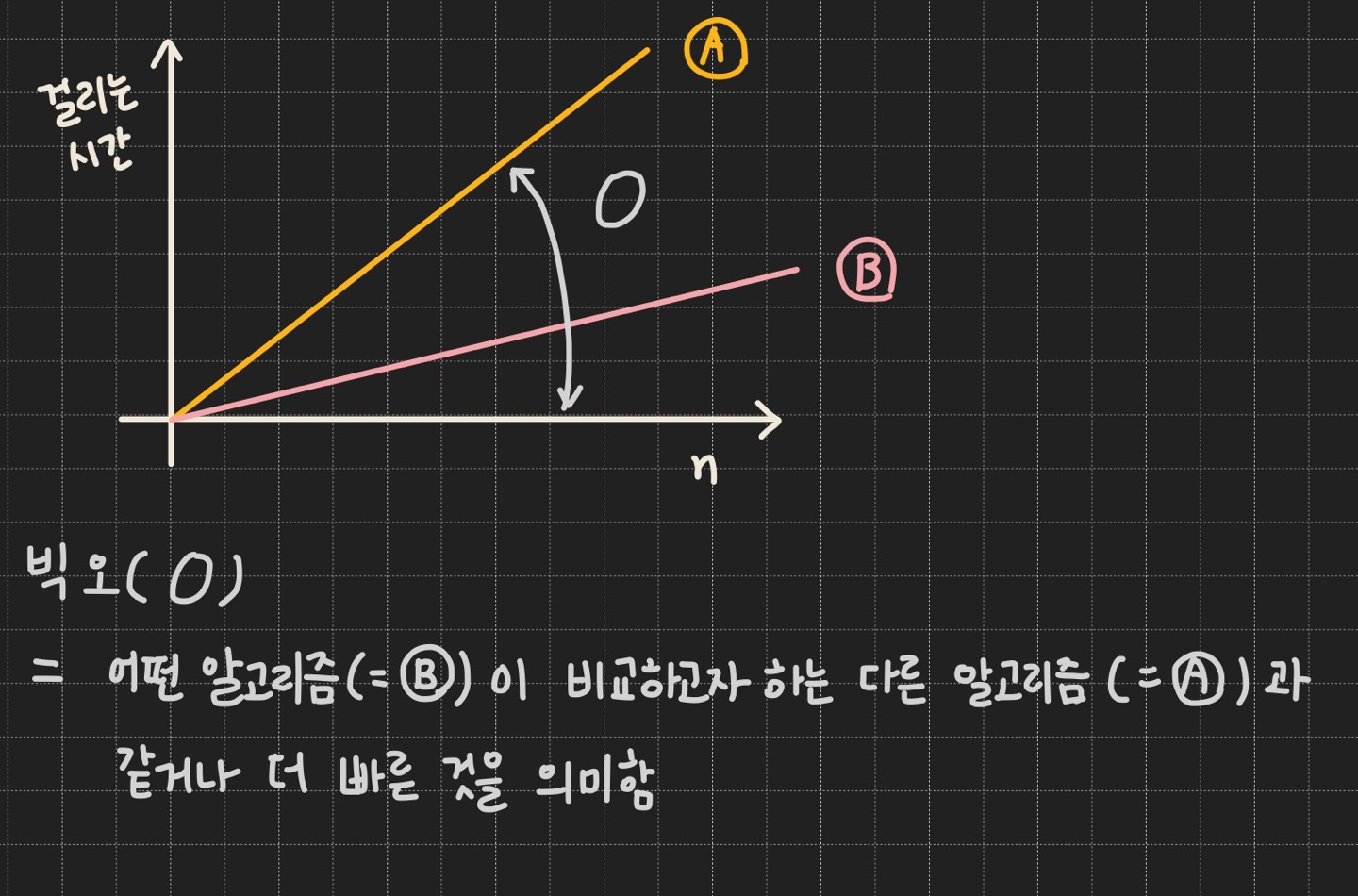
- 빅 오 복잡도란?
→ 어떤 알고리즘이 비교하고자 하는 다른 알고리즘과 같거나 더 빠른 것을 의미함
- 만약 그래프 B 알고리즘이 그래프 A와 같다면
→ 이때는 세타 복잡도라고 부름
- 즉, 세타는 같은 정도로 증가한다는 의미임
- 빅 오메가 복잡도란?
→ 어떤 알고리즘이 비교하고자 하는 다른 알고리즘과 같거나 더 느린 것을 의미함
- 리틀 오 복잡도란?
→ 빠르지만 같지는 않다는 의미임
→ 만약 어떤 알고리즘이 다른 알고리즘보다 작은 복잡도를 가지고 있고 + 그 알고리즘과 같아질 수는 없다면 리틀 오 복잡도를 가지고 있다고 표현함
- 리틀 오메가 복잡도란?
→ 느리지만 같지는 않다는 의미임
→ 만약 어떤 알고리즘이 다른 알고리즘보다 큰 복잡도를 가지고 있고 + 그 알고리즘과 같아질 수는 없다면 리틀 오 복잡도를 가지고 있다고 표현함
- 이 용어들이 굉장히 중요하기 때문에 다시 한번 쉽게 정리함
→ 우리는 "빅(Big)"과 "리틀(Little)", "오(O)"와 "오메가(Ω, ω)"를 잘 구분해야함

- 복잡도 정리
→ 빅 오 복잡도(O) : 어떤 알고리즘과 비교 했을 때 같거나, 빠름
→ 리틀 오 복잡도(o) : 어떤 알고리즘과 비교 했을 때 빠름
→ 빅 오메가 복잡도(Ω) : 어떤 알고리즘과 비교 했을 때 같거나, 느림
→ 리틀 오메가 복잡도(ω) : 어떤 알고리즘과 비교 했을 때 느림
→ 세타 복잡도(θ) : 어떤 알고리즘과 비교 했을 때 같음
2. 빅 오 표기법 예시
[개요]
- 예시를 통해 빅 오 표기법으로 알고리즘 효율성 비교하기
[내용]
- 아래의 식은 성립하는가? (True or False?)
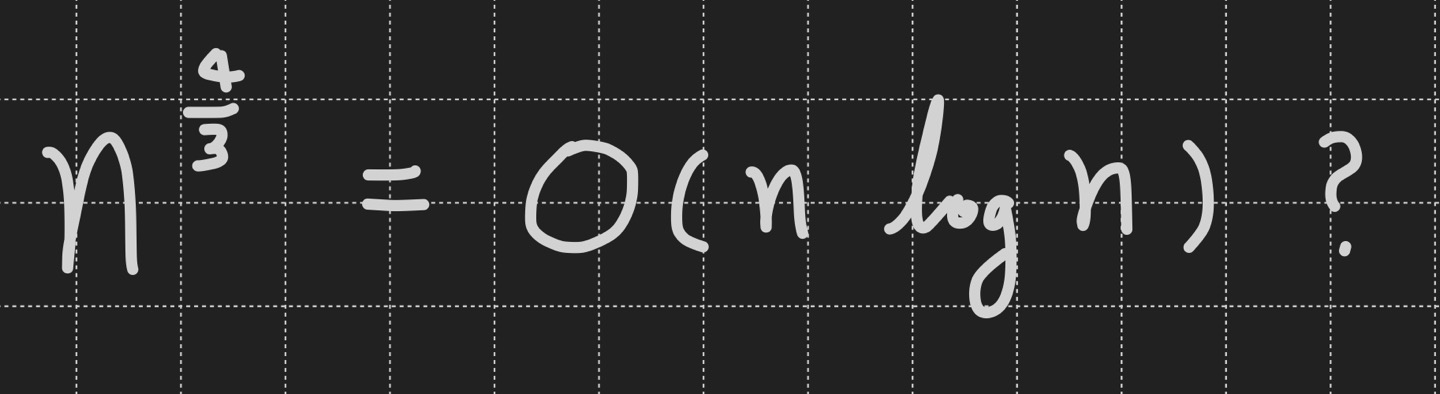
- 이 문제의 답을 찾기 위해 좀 더 쉽게 접근해보자
→ 아래의 식을 비교한다고 가정

→ 이때 우리의 관심사는 n=1, 2, 3... 등 n이 유한한 숫자일 때의 상황이 아님
→ n이 무한대(∞)일 때의 상황에 관심을 가져야함
* n이 1이거나 2인 것은 알고리즘의 효율을 비교하지 않아도 쉽게 처리되는 것이기 때문
* 우리는 n(입력한 데이터의 크기)이 1000, 10000, 1000000... 등으로 굉장히 클 때
어떤 알고리즘이 더 효율적으로 작업을 처리하는지 찾아야함
→ 하지만 문제의 답을 쉽게 찾기 위해 n=1000으로 가정해서 비교해봄

→ 그래프로 그려보면 아래와 같이 나올 수 있음

- 그렇다면 n^(4/3)은 O(nlogn)이 될 수 있는가?
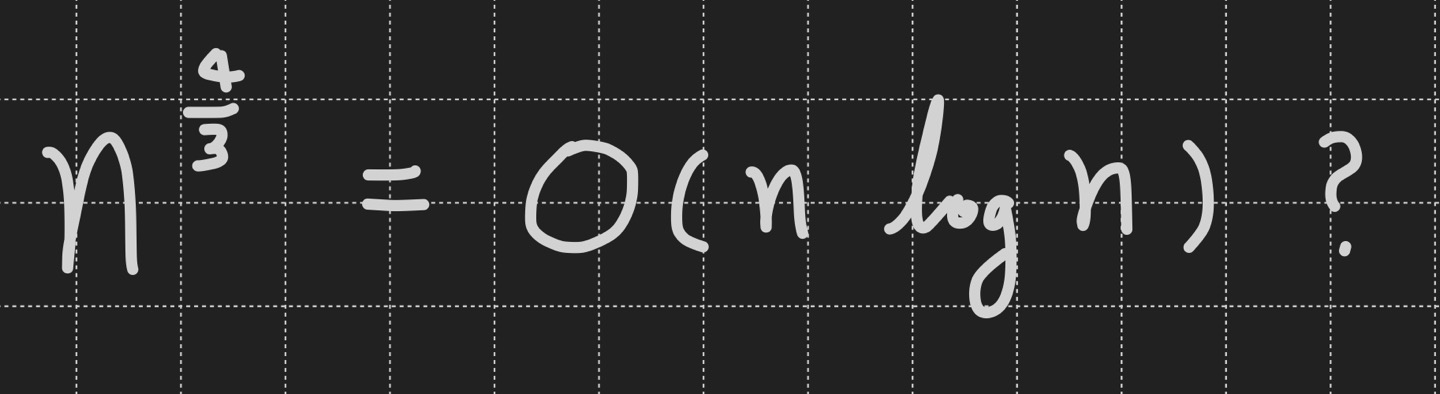
→ 정답은 "아니오"임
- 우선 문제를 해석하고 그래프를 해석해야함
→ O(nlogn)이라는 항은 빅 오 복잡도 이기 때문에 "소괄호 안의 식보다 같거나 빠르다"라는 의미임
→ 즉, O(nlogn)은 "nlogn보다 같거나 빠르다"라는 뜻
→ 그래프에 표시하면 아래와 같이 표현됨
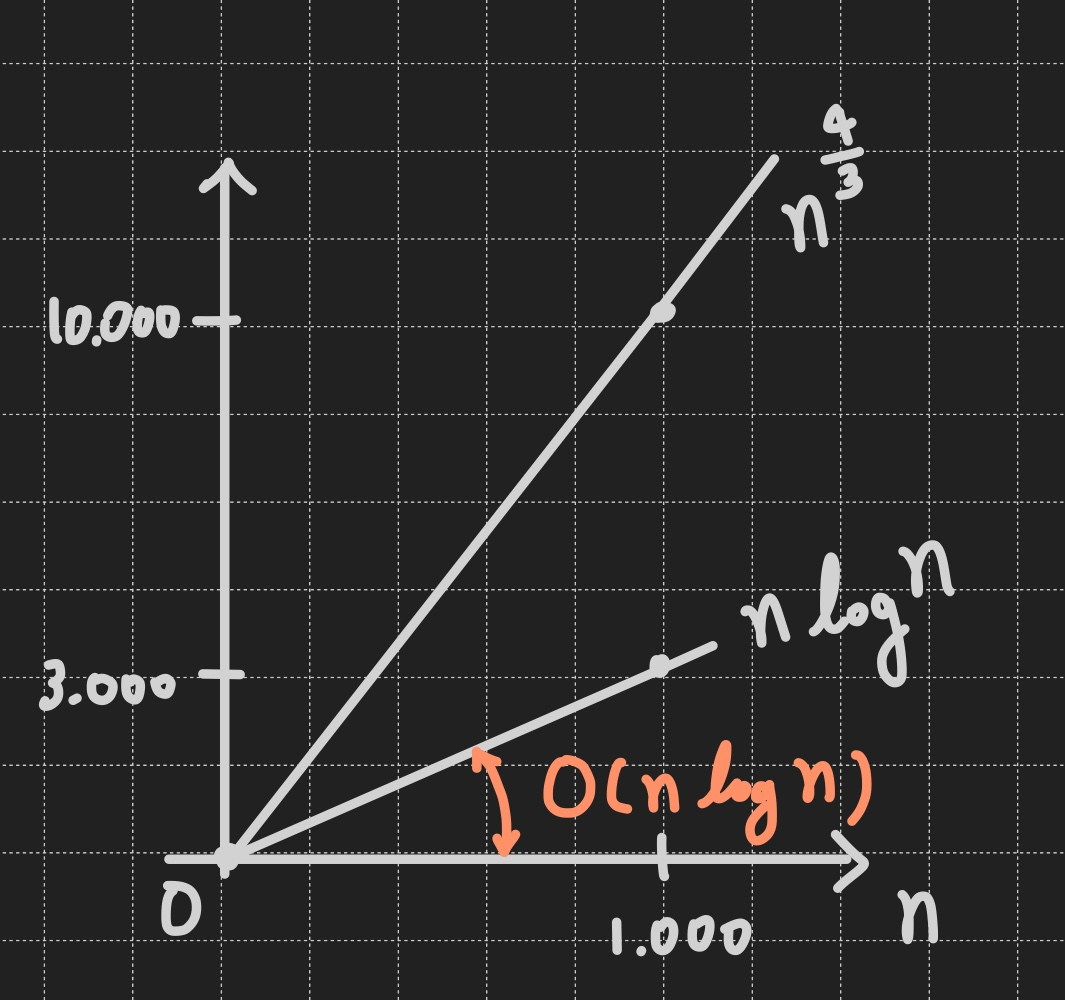
→ 문제에서는 n^(4/3)이 O(nlogn)인지 묻고 있음
즉, n^(4/3)이 nlogn과 같거나 빠른지 묻고 있는 것
→ 그래프를 보면 알 수 있듯이 n^(4/3)은 O(nlogn)의 범위에 포함되지 않음
→ 따라서 답은 "거짓(False)"임
- 유의. 위의 방법이 이런 문제를 해결하는 가장 쉬운 계산법이지만 이 방법을 사용하지 못하는 경우도 몇가지 있음
→ 사실 이런 문제를 해결하는데는 로피탈 법칙을 사용해야함 (공학에서 수학의 중요성을 또 한번 느낌..)
※ 헛갈리지 말아야 하는 부분
- 그래프만 보면 n^3 이 n보다 더 효율이 좋아 보이지만
- 우리는 x축과 y축의 의미를 잘 생각해야함
→ y축이 "소요되는(걸리는, 필요한) 시간"임

확실히 공학 수학이 굉장히 중요한 것 같다.
지금 자료구조만 공부해봐도 극한, 미적분, 지수/로그 등을 리마인드할 필요성이 있다고 느껴지는데
전부 대학교 때까지 공부하고 손에서 놓았기 때문에... 지금은 기억 한조각 남아있지 않다.
수학 개념책을 다시 꺼낼 때가 된 것 같다.
'3. Computer Science 공부 > 자료구조' 카테고리의 다른 글
| [자료구조] 네이버 부스트코스 '자바로 구현하고 배우는 자료구조' 공부 필기 (6) (0) | 2021.12.01 |
|---|---|
| [자료구조] 네이버 부스트코스 '자바로 구현하고 배우는 자료구조' 공부 필기 (5) (0) | 2021.11.30 |
| [자료구조] 네이버 부스트코스 '자바로 구현하고 배우는 자료구조' 공부 필기 (4) (0) | 2021.11.23 |
| [자료구조] 네이버 부스트코스 '자바로 구현하고 배우는 자료구조' 공부 필기 (3) (0) | 2021.11.22 |
| [자료구조] 네이버 부스트코스 '자바로 구현하고 배우는 자료구조' 공부 필기 (1) (0) | 2021.11.05 |




