회고록 블로그
[공부 필기] Java 기본 공부하기 (3) 본문
원래 참고하고 있는 책이 너무 노잼이라 공부를 이어갈 수가 없다.
그래서 윤성우 선생님 강의를 들으면서 필요한 부분만 정리하기로 했다.
윤성우 선생님의 강의는 카페 가입 시 들을 수 있다. (자바 뿐만 아니라 파이썬이나 디자인패턴 강의도 있는 듯 하다)
https://cafe.naver.com/cstudyjava
윤성우의 프로그래밍 스터디그룹 [C/... : 네이버 카페
윤성우의 스터디 공간입니다. C와 JAVA를 공부하시는 분들은 모두 들어오세요. ^^
cafe.naver.com
1. javac
→ JDK에 있는 java 컴파일러
2. 명령 프롬프트로 javac.exe와 java.exe 이용한 자바 코드 실행
→ 참고로 java.exe(자바 런처)는 JVM을 실행시키고 그 곳에 클래스 파일을 얹어놓는 역할을 함
→ 이후 JVM이 클래스 파일을 한문장 한문장 해석함
3. 소스코드 분석
→ 클래스(class) 안에 메소드 존재함
4. 실수
→ 정수는 오차 없는 표현이 가능하지만, 실수는 오차 없는 표현이 거의 불가능함
단일 값만 생각하면 원래 생각했던 값과 큰 오차는 아닐 수 있지만,
무수히 많은 실수들을 더하고, 빼고 하다보면 오차가 크게 벌어날 수 있음
→ 왜 오차가 생길까?
* 컴퓨터가 실수를 저장하는 방법 때문.
* 컴퓨터는 2진수로만 값을 표현할 수 있는데
* 컴퓨터가 실수를 표현하는 방식에는 '고정소수점'과 '부동소수점'이 있음
* 대부분 컴퓨터는 부동 소수점 방식으로 실수를 표현하는데, IEEE 754 표준 부동소수점을 사용함



* 위의 계산 그림에서도 알 수 있듯이 0.3을 2진수로 표현하려면 소수점 자리가 무한대로 계속 되어야 하는데
float나 double형은 비트수가 정해져 있다보니 결국 비트수에 맞춰 잘려야 함
그러다보니 당연히 오차가 발생할 수 밖에 없음
* 만약 0.625 였다면 오차가 발생하지 않았을 것임 0.625는 2진수로 표현하면 0.001으로 딱 떨어지기 때문

* 참고자료: http://tcpschool.com/java/java_datatype_floatingPointNumber
→ 하지만 실수의 오차를 해결하기 위한 나름의 방법들이 있음(나중에 배움)
5. 기본 자료형
→ 정수의 사칙연산은 int형으로 처리됨
* 아래 #1 참고
→ float가 표현할 수 있는 범위보다 double이 표현할 수 있는 값의 범위가 더 넓은데
'표현할 수 있는 값이 넓다'는 의미이기도 하지만, 'double 데이터 타입은 float형보다 더 오차가 적다'는 의미이기도 함
* 위에서 실수는 오차 없이 표현이 불가능하다고 했음
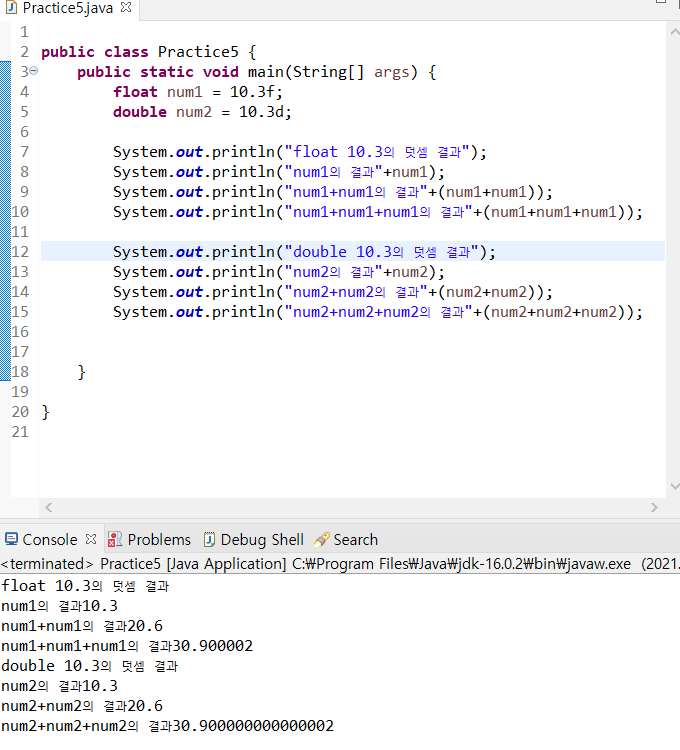
* float는 소수점 이하 6자리까지는 오차가 발견되지 않음(소수점 이하 7자리부터 오차가 발견될 가능성이 있음)
* double은 소수점 이하 15자리까지는 오차가 발견되지 않음(소수점 이하 16자리부터 오차가 발견될 가능성이 있음)
* 오차는 연산을 한 후 리셋되는게 아니라 계속 누적되기 때문에,
아래와 같이 첫번째나 두번째 덧셈에서 보이지 않더라도 세번째에서는 보일 수도 있고 안 보일 수도 있음
그러므로 오차를 항상 염두하며 사용해야 함
* 따라서, float와 double의 자료형 선택 기준은 '표현할 수 있는 범위' 보다는 '정밀도'임
→ 문자형은 2바이트로 표현함
* 가장 보편적인 기준은 Unicode임 (자바도 Unicode를 채택하고 있음)
* JVM과 자바 컴파일러에게는 유니코드가 이미 심어져 있는데, 사용자가 문자를 입력하면 그들이 유니코드 정보에서 문자를 찾아 '유니코드 값(숫자)'으로 변환 후 저장함 (따라서 char에는 유니코드값이 저장됨)
* char 데이터 타입은 '문자'를 저장할 때 사용함. 즉, JVM/컴파일러와 char은 문자로 해석하라는 약속을 함.
#1. 두개의 short형 값을 더하면 에러 발생?

num1과 num2는 데이터 타입이 short이고, 둘을 더하면 에러가 발생한다.
에러의 내용은 cannot convert from int to short 즉, int에서 short로 변환이 불가능하다는 에러이다.
※ 사전 지식
Java는 메모리 크기가 '작은' 데이터 타입에서 메모리 크기가 '큰' 데이터 타입으로 변환될 때에는 자동 형변환이 일어난다.
반대로 '큰' 데이터 타입에서 '작은' 데이터 타입으로 변환될 때는 강제 형변환이 필요하다.
JVM은 num1 변수와 num2 변수를 더할 때, int형으로 변환 후 덧셈을 진행한다.
아래와 같은 계산이 있다고 가정하자.
1번 문제. 1(1바이트 정수) + 2(1바이트 정수)
2번 문제. 128(2바이트 정수) + 129(2바이트 정수)
3번 문제. 1(1바이트 정수)+32768(4바이트 정수)
만약 사람이나 컴퓨터나 각각 바이트에 맞는 덧셈을 한다고 가정하자.
사람은 머릿속으로 쉽게 계산하면 되지만
컴퓨터는 이 숫자가 1바이트인지, 2바이트인지, 4바이트인지 체크하고
1바이트와 2바이트의 덧셈이면? 1바이트를 2바이트로 만들어주고 덧셈을 하고
1바이트와 4바이트의 덧셈이면? 1바이트를 4바이트로 만들어주고 덧셈을 하는 등 경우의 수를 만들어 복잡한 과정을 거쳐야한다.
그러다보면 성능이 저하 되어버리는 문제가 생김.
그래서 성능 향상을 위해서 컴퓨터는'이 데이터가 1바이트이든지, 2바이트이든지, 4바이트이든지 상관없이 모두 4바이트로 변환하고 더한다' 라는 컨셉으로 계산을 하게 된다.
※ 각각의 경우에 맞춰 동작하면 사람 입장에서는 좋겠지만 컴퓨터 입장에서는 성능 저하로 인해 굉장히 부담스러운 일이라고 함
그래서, 성능 저하를 최소화 하며 동작하기 위해 굳이 4바이트로 모두 맞춘 것
※ 왜 4바이트이냐면, 가장 보편적으로 사용하는 바이트이기 때문이라고 한다.
따라서, 위의 코드에서 두 개의 short형(2바이트) 변수을 더하려면 int형(4바이트)으로 먼저 변환이 되어야 한다.
num1과 num2 변수가 int형으로 변환되고 덧셈이 되는 것.
여기까지는 문제가 없는데,
문제가 되는 부분은 이 더한 값이 result 변수(short형임)에 대입되는 부분 때문이다.
num1+num2의 값은 int형이 되어버렸는데
result 변수는 short형이다보니 'int형 데이터를 short형에 넣을 수 없다'라고 에러를 보내주는 것.
(short(작은 데이터 타입)에서 int(큰 데이터 타입)로 갈 때는 자동 형변환 되지만
int(큰 데이터 타입)에서 short(작은 데이터 타입)로 갈 때는 강제 형변환이 필요함)
또한 num1+num2의 값이 short형의 범위에 포함되는 숫자라 할지라도
JVM은 무조건 int형으로 반환한다.
('num1+num2의 값이 short형의 범위에 포함되는지 체크하고 ▶ short형의 범위에 들어가면 ▶ short형으로 형변환'
이런 과정을 JVM이 처리하면 성능이 너무 저하되기 때문에
JVM은 num1+num2의 값이 어느 데이터 타입에 포함되는지 체크하지 않음)
(num1+num2)를 short형으로 강제 형변환을 시켜주거나,
result 변수를 int형으로 선언해주거나,
모든 변수를 int형으로 변경해주면 되는데 강의에서는 "모든 변수를 int형으로 변경"하는 것을 추천했음.
왜냐하면,
어차피 num1+num2를 처리 할 때 컴퓨터는 num1과 num2를 각각 int형으로 변환하는데
굳이 num1과 num2를 short형으로 선언해서
컴퓨터에게 short형을 int형으로 변환하는 과정을 겪게 할 필요가 없기 때문이다.
처음부터 num1과 num2를 int형으로 선언해서 이 과정을 없애버리면
성능 향상에도 도움이 된다고 한다.
※ 메모리의 공간을 아껴야 하는 프로그램이거나,
(더하기, 빼기 등의) 연산이 아니라 데이터 저장이 목적인 프로그램이라면 short, byte 등 데이터 타입을 써도 되지만
나중에 연산할 때는 가지고 와서 int로 강제 형변환 하거나 등을 해주어야 함
출처 : 윤성우 선생님, 열혈 Java 강의, https://cafe.naver.com/cstudyjava
'2. 프로그래밍 언어 공부 > Java' 카테고리의 다른 글
| [공부 쉬어가기] Java: 왜 복합 대입 연산자는 형변환 에러가 발생하지 않을까 (0) | 2021.09.01 |
|---|---|
| [공부 필기] Java 기본 공부하기 (4) (0) | 2021.09.01 |
| [공부 필기] Java 기본 공부하기 (2) (0) | 2021.08.26 |
| [공부 필기] Java 기본 공부하기 (1) (0) | 2021.08.20 |
| [공부 필기] Java 기본 공부하기 - 프롤로그 (0) | 2021.08.19 |




